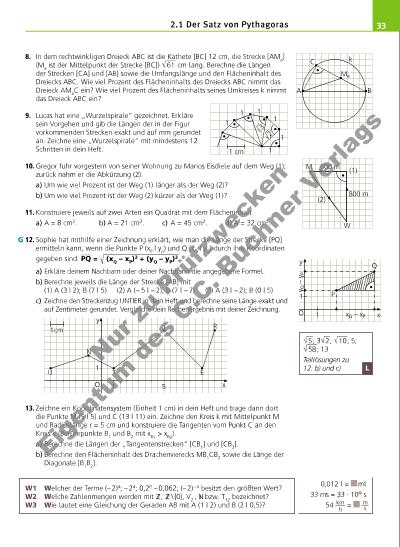
332.1 Der Satz von Pythagoras 8. In dem rechtwinkligen Dreieck ABC ist die Kathete [BC] 12 cm, die Strecke [AMa] (Ma ist der Mittelpunkt der Strecke [BC]) √ ___ 61 cm lang. Berechne die Längen der Strecken [CA] und [AB] sowie die Umfangslänge und den Flächeninhalt des Dreiecks ABC. Wie viel Prozent des Flächeninhalts des Dreiecks ABC nimmt das Dreieck AMaC ein? Wie viel Prozent des Flächeninhalts seines Umkreises k nimmt das Dreieck ABC ein? 9. Lucas hat eine „Wurzelspirale“ gezeichnet. Erkläre sein Vorgehen und gib die Längen der in der Figur vorkommenden Strecken exakt und auf mm gerundet an. Zeichne eine „Wurzelspirale“ mit mindestens 12 Schritten in dein Heft. 10. Gregor fuhr vorgestern von seiner Wohnung zu Marios Eisdiele auf dem Weg (1); zurück nahm er die Abkürzung (2). a) Um wie viel Prozent ist der Weg (1) länger als der Weg (2)? b) Um wie viel Prozent ist der Weg (2) kürzer als der Weg (1)? 11. Konstruiere jeweils auf zwei Arten ein Quadrat mit dem Flächeninhalt a) A = 8 cm2. b) A = 21 cm2. c) A = 45 cm2. d) A = 32 cm2. 12. Sophie hat mithilfe einer Zeichnung erklärt, wie man die Länge der Strecke [PQ] ermitteln kann, wenn die Punkte P (xP | yp) und Q (xQ | yQ) durch ihre Koordinaten gegeben sind: ___ PQ = √ ___________________ (xQ – xP) 2 + (yQ – yP) 2 . a) Erkläre deinem Nachbarn oder deiner Nachbarin die angegebene Formel. b) Berechne jeweils die Länge der Strecke [AB] mit (1) A (3 | 2); B (7 | 5) (2) A (− 5 | − 2); B (7 | − 7) (3) A (3 | − 2); B (0 | 5) c) Zeichne den Streckenzug UNTIER in dein Heft und berechne seine Länge exakt und auf Zentimeter gerundet. Vergleiche dein Rechenergebnis mit deiner Zeichnung. 13. Zeichne ein Koordinatensystem (Einheit 1 cm) in dein Heft und trage dann dort die Punkte M (5 | 5) und C (13 | 11) ein. Zeichne den Kreis k mit Mittelpunkt M und Radiuslänge r = 5 cm und konstruiere die Tangenten vom Punkt C an den Kreis k (Berührpunkte B1 und B2 mit xB1 > xB2). a) Berechne die Längen der „Tangentenstrecken“ [CB1] und [CB2]. b) Berechne den Flächeninhalt des Drachenvierecks MB1CB2 sowie die Länge der Diagonale [B1B2]. W1 Welcher der Terme (– 2)4; – 24; 0,20 – 0,062; (– 2) – 4 besitzt den größten Wert? W2 Welche Zahlenmengen werden mit , \ {0}, V2 , bzw. T12 bezeichnet? W3 Wie lautet eine Gleichung der Geraden AB mit A (1 | 2) und B (2 | 0,5)? √ __ 5 ; 3 √ __ 2 ; √ ___ 10 ; 5; √ ___ 58 ; 13 Teillösungen zu 12. b) und c) k Ma C A B 600 mM W (2) (1) 800 m 1 1 1 11 1 1 cm 2 3 xO 1 y 1 xQ – xP y Q – y P P Q xO 1 y 1 5 I E R TU N 1cm G L 0,012 l = ml 33 ms = 33 · 10 s 54 km ___ h = m __ s Nu r z u Pr üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs