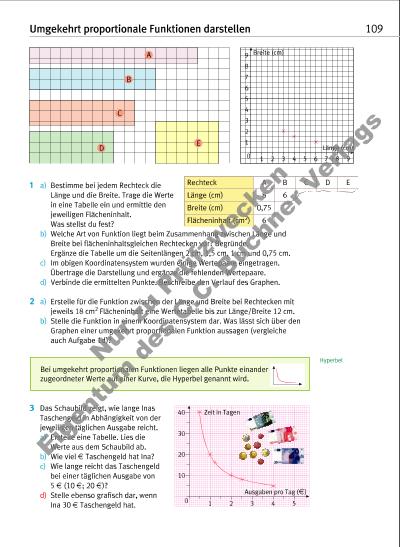
Umgekehrt proportionale Funktionen darstellen 109 1 a) Bestimme bei jedem Rechteck die Länge und die Breite. Trage die Werte in eine Tabelle ein und ermittle den jeweiligen Flächeninhalt. Was stellst du fest? b) Welche Art von Funktion liegt beim Zusammenhang zwischen Länge und Breite bei flächeninhaltsgleichen Rechtecken vor? Begründe. Ergänze die Tabelle um die Seitenlängen 2 cm, 1,5 cm, 1 cm und 0,75 cm. c) Im obigen Koordinatensystem wurden einige Wertepaare eingetragen. Übertrage die Darstellung und ergänze die fehlenden Wertepaare. d) Verbinde die ermittelten Punkte. Beschreibe den Verlauf des Graphen. 2 a) Erstelle für die Funktion zwischen der Länge und Breite bei Rechtecken mit jeweils 18 cm2 Flächeninhalt eine Wertetabelle bis zur Länge/Breite 12 cm. b) Stelle die Funktion in einem Koordinatensystem dar. Was lässt sich über den Graphen einer umgekehrt proportionalen Funktion aussagen (vergleiche auch Aufgabe 1d)? 1 Länge (cm) 1 2 3 4 5 2 3 4 5 6 7 8 9 6 7 8 9 Breite (cm) 0 3 Das Schaubild zeigt, wie lange Inas Taschengeld in Abhängigkeit von der jeweiligen täglichen Ausgabe reicht. a) Erstelle eine Tabelle. Lies die Werte aus dem Schaubild ab. b) Wie viel “ Taschengeld hat Ina? c) Wie lange reicht das Taschengeld bei einer täglichen Ausgabe von 5 “ (10 “; 20 “)? d) Stelle ebenso grafisch dar, wenn Ina 30 “ Taschengeld hat. Hyperbel 10 1 20 30 2 3 4 Zeit in Tagen Ausgaben pro Tag (2) 40 0 5 Bei umgekehrt proportionalen Funktionen liegen alle Punkte einander zuge ordneter Werte auf einer Kurve, die Hyperbel genannt wird. Rechteck A B C D E Länge (cm) 8 6 Breite (cm) 0,75 Flächeninhalt (cm2) 6 A B C D E Nu r z u P üf zw ec ke n Ei ge nt um d es C .C . B uc hn er V er la gs