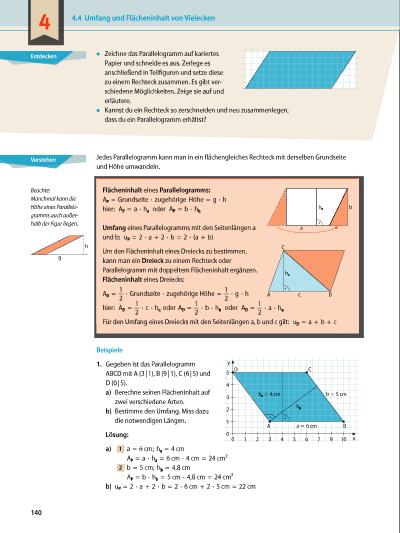
Entdecken ▪▪ Zeichne das Parallelogramm auf kariertes Papier und schneide es aus. Zerlege es anschließend in Teil figuren und setze diese zu einem Rechteck zusammen. Es gibt ver­ schiedene Möglichkeiten. Zeige sie auf und erläutere. ▪▪ Kannst du ein Rechteck so zerschneiden und neu zusammenlegen, dass du ein Parallelogramm erhältst? Jedes Parallelogramm kann man in ein flächengleiches Rechteck mit derselben Grundseite und Höhe umwandeln. Beispiele 1. Gegeben ist das Parallelogramm ABCD mit A (3 | 1), B (9 | 1), C (6 | 5) und D (0 | 5). a) Berechne seinen Flächeninhalt auf zwei verschiedene Arten. b) Bestimme den Umfang. Miss dazu die notwendigen Längen. Lösung: a) 1 a = 6 cm; ha = 4 cm AP = a · ha = 6 cm · 4 cm = 24 cm2 2 b = 5 cm; hb = 4,8 cm AP = b · hb = 5 cm · 4,8 cm = 24 cm2 b) uP = 2 · a + 2 · b = 2 · 6 cm + 2 · 5 cm = 22 cm Flächeninhalt eines Parallelogramms: AP = Grundseite · zugehörige Höhe = g · h hier: AP = a · ha oder AP = b · hb Umfang eines Parallelogramms mit den Seitenlängen a und b: uP = 2 ∙ a + 2 · b = 2 · (a + b) Um den Flächeninhalt eines Dreiecks zu bestimmen, kann man ein Dreieck zu einem Rechteck oder Parallelogramm mit doppeltem Flächeninhalt ergänzen. Flächeninhalt eines Dreiecks: AD = 1 __ 2 · Grundseite · zugehörige Höhe = 1 __ 2 · g · h hier: AD = 1 __ 2 · c · hc oder AD = 1 __ 2 · b · hb oder AD = 1 __ 2 · a · ha Für den Umfang eines Dreiecks mit den Seitenlängen a, b und c gilt: uD = a + b + c a bha A B C hc c h g Beachte: Manchmal kann die Höhe eines Parallelo­ gramms auch außer­ halb der Figur liegen. hb ha = 4 cm x 0 0 1 2 3 4 5 6 7 9 10 y 1 2 3 4 5 A B CD b = 5 cm a = 6 cm Verstehen 4.4 Umfang und Flächeninhalt von Vielecken 140 4