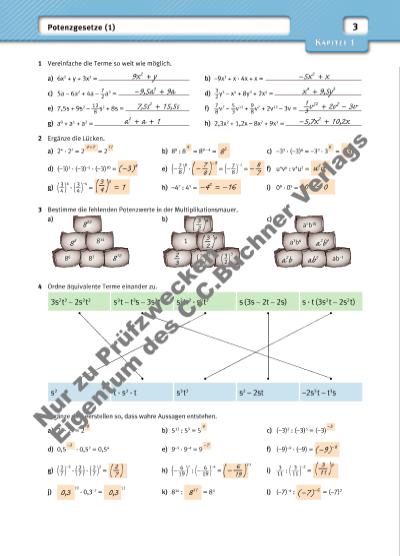
Kapitel 1 3Potenzgesetze (1) 1 Vereinfache die Terme so weit wie möglich. a) 6x2 + y + 3x2 = b) –9x2 + x · 4x + x = c) 5a – 6a2 + 4a – 7 __ 2 a 2 = d) 3 __ 2 y 3 – x4 + 8y3 + 2x4 = e) 7,5s + 9s2 – 12 ___ 8 s 2 + 8s = f) 7 __ 8 v 7 – 5 __ 3 v 12 + 9 __ 8 v 7 + 2v12 – 3v = g) a0 + a1 + a2 = h) 2,3x2 + 1,2x – 8x2 + 9x1 = 2 Ergänze die Lücken. a) 24 · 27 = 2 = 2 b) 89 : 8 = 89 – 4 = c) –33 · (–3)6 = –33 · 3 = d) (–3)3 · (–3)–5 · (–3)10 = e) ( – 7 __ 8 ) 8 · = ( – 7 __ 8 ) –1 = f) u4v6 : v4u2 = g) ( 3 __ 4 ) 4 · ( 3 __ 4 ) –4 = h) –47 : 45 = i) 09 · 05 = 3 Bestimme die fehlenden Potenzwerte in der Multiplikationsmauer. a) b) c) 4 Ordne äquivalente Terme einander zu. 5 Ergänze die Leerstellen so, dass wahre Aussagen entstehen. a) 23 · 25 = 2 b) 513 : 59 = 5 c) (–3)2 : (–3)5 = (–3) d) 0,5 · 0,57 = 0,54 e) 9–3 · 9–4 = 9 f) (–9)–9 · (–9) = g) ( 2 __ 7 ) –3 · ( 2 __ 7 ) · ( 2 __ 7 ) 3 = h) ( – 6 ___ 19 ) 7 : ( – 6 ___ 19 ) –4 = i) 3 ___ 11 : ( 3 ___ 11 ) –2 = j) 19 · 0,3–7 = 12 k) 814 : = 83 l) (–7)–4 : = (–7)2 814 86 82 1 ( 2 __ 3 ) –1 ( 3 __ 2 ) 3 a5b10 a3b6 ab–1 3s2 t2 – 2s2 t2 s3 t – t3s – 3s3 t s2 t –2 · s0 t2 s (3s – 2t – 2s) s · t (3s2 t – 2s2 t) s2 t · s2 · t s3 t2 s2 – 2st –2s3 t – t3s 9x2 + y –5x2 + x –9,5a2 + 9a x4 + 9,5y3 7,5s2 + 15,5s 1 __ 3 v 12 + 2v7 – 3v a2 + a + 1 –5,7x2 + 10,2x 4+7 8 –3 –7 (–9)–8 0,3 0,3 811 (–7)–6 ( 3 __ 11 ) 3 ( – 6 __ 19 ) 11 ( 2 __ 7 ) 4 –3 11 4 85 (–3)8 ( 3 __ 4 ) 0 = 1 –42 = –16 014 = 0 ( – 7 __ 8 ) –9 – 8 __ 7 u2v2 6 –39 822 88 812 ( 3 __ 2 ) 4 ( 3 __ 2 ) 4 2 __ 3 a2b4 a2b ab5 Nu r z u Pr üf zw ec ke n Ei g nt um d es C .C .B uc hn er V er la gs